We have so far two spaces for modeling tones (the circle of fifths, and the more complex but satisfying torus space), and a number of spaces for modelling colors. Let's now consider appropriate mappings between the spaces.
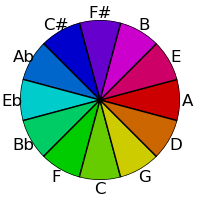
The key feature of the tone spaces is that they are cyclical. The only color space that is directly cyclical is the HSV color space, in the hue dimension. As a first attempt, let's map the circle of fifths onto the hue dimension whilst keeping saturation and value fixed.
| Fifths Order | Semitone Order | Torus Plot |
|---|---|---|
 |  |  |
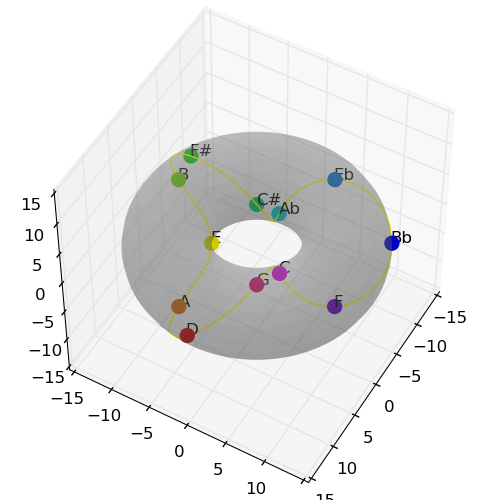
This has some obvious advantages - related tones seem fairly similar etc - along with the logical disadvantage that since the circle of fifths maps major seconds as closer than major thirds, these differences come through in the color space. This is because we are mapping the γ angle in the torus to hue, but doing nothing with the θ angle.
It would be ideal if the color space had an additional circular dimension, but it does not. Trying to use the other dimensions to approximate them is not satisfying - the consistent strength of the colors in the simpler mapping seems to be of more advantage than the variation in shades shown here:
Another possibility is to use something other than color to represent the θ angle in the torus; a simple example is an actual rotation of a line
| Fifths Order | Semitone Order |
|---|---|
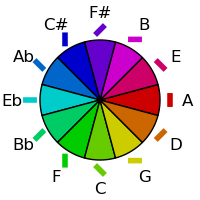 | 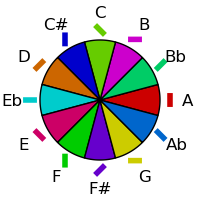 |
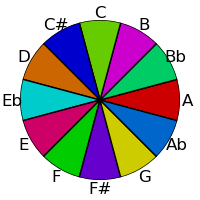
Visually, there is still an issue though - the greens are not as spread out as the other colors and are harder to distinguish. This can be addressed by using the Lab color space to select colors with the same saturation and value, but with hue values chosen to optimize the distance in that space. However, the Lab delta spaces still does not achieve anything uniform perceptual difference over large distances; using defined Delta-E functions on this space can improve the distribution as shown at right (and these deltas will be used to spread the hues from here onwards):
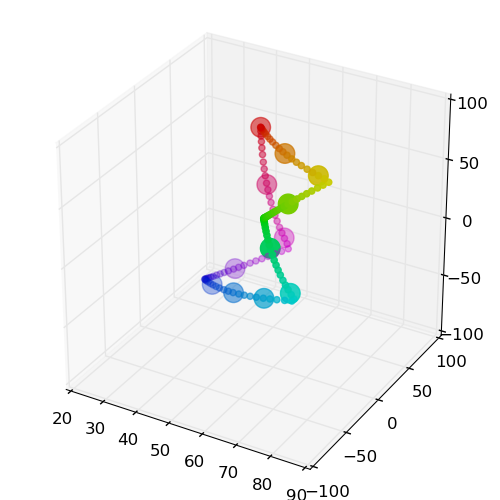
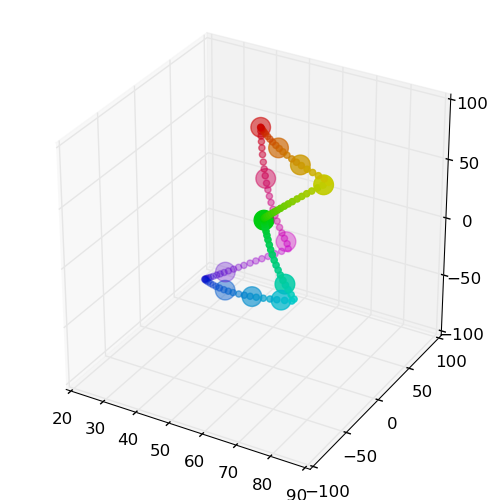
These selections then result in more easily differentiated hues:
| Fifths Order | Torus Plot |
|---|---|
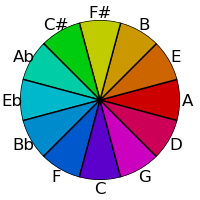 | 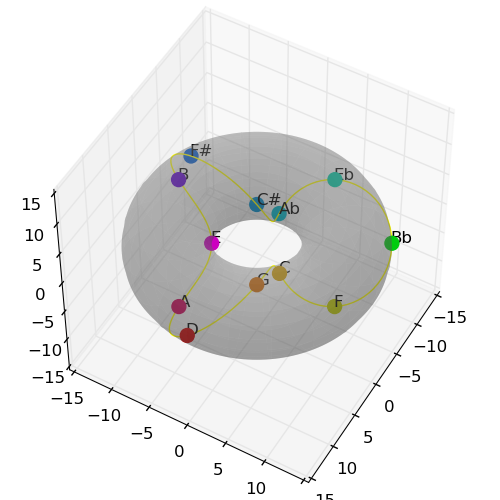 |
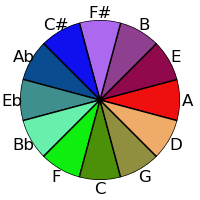
Combining this with the rotation we had earlier gives the following:
| Fifths Order | Semitone Order |
|---|---|
 | 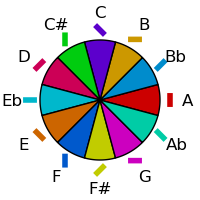 |
© David Fraser 2013